MCMC샘플링으로 배달시간 예측하기

import numpy as np  
import matplotlib.pyplot as plt  
  
# 데이터 생성 파라미터  
n_samples = 1000  
np.random.seed(42)  
  
# 시간대에 따른 배달 시간 설정  
def generate_delivery_time(hour, rider_acceptance_rate, num_riders):  
    base_time = 25  # 전체 배달 시간 평균 25분  
    # 점심, 저녁 시간대 배달 시간 증가  
    if 11 <= hour <= 13 or 18 <= hour <= 20:    
        variance = np.random.normal(loc=8, scale=2)  # 배달시간이 늘어짐  
    else:    
        variance = np.random.normal(loc=4, scale=1)  # 기본 배달시간  
    # 라이더 배차 수락율과 규모에 따른 배달시간 조정  
    rider_effect = 1 / (rider_acceptance_rate * num_riders + 1)  
      
    return base_time + variance * rider_effect  
  
# 가상의 데이터 생성  
hours = np.random.randint(0, 24, n_samples)  
rider_acceptance_rates = np.random.uniform(0.5, 1.0, n_samples)  
num_riders = np.random.randint(10, 50, n_samples)  
  
delivery_times = np.array([generate_delivery_time(hour, rate, riders)   
                           for hour, rate, riders in zip(hours, rider_acceptance_rates, num_riders)])  
  
# Metropolis-Hastings MCMC 구현  
def metropolis_hastings(delivery_times, iterations=10000, prior_mu=25, prior_sigma=5):  
    # 초기 상태 설정  
    current_state = np.mean(delivery_times)  
    states = [current_state]  
      
    for _ in range(iterations):  
        # 새로운 제안 상태 생성  
        proposed_state = np.random.normal(current_state, 1.0)  
          
        # 수락 확률 계산 (사전분포 반영)  
        current_likelihood = np.sum(-0.5 * (delivery_times - current_state) ** 2)  
        proposed_likelihood = np.sum(-0.5 * (delivery_times - proposed_state) ** 2)  
          
        # 사전분포 적용  
        current_prior = -0.5 * ((current_state - prior_mu) ** 2) / (prior_sigma ** 2)  
        proposed_prior = -0.5 * ((proposed_state - prior_mu) ** 2) / (prior_sigma ** 2)  
          
        # 수락 비율 계산  
        acceptance_ratio = np.exp(proposed_likelihood + proposed_prior - current_likelihood - current_prior)  
          
        # 새로운 상태를 수락할지 결정  
        if np.random.rand() < acceptance_ratio:  
            current_state = proposed_state  
              
        states.append(current_state)  
      
    return np.array(states)  
  
# MCMC 샘플링 수행 (사전분포 적용)  
prior_mu = 25  # 사전분포의 평균  
prior_sigma = 5  # 사전분포의 표준편차  
mcmc_samples = metropolis_hastings(delivery_times, iterations=10000, prior_mu=prior_mu, prior_sigma=prior_sigma)  
  
# 결과 시각화  
plt.hist(mcmc_samples, bins=50, density=True, alpha=0.7)  
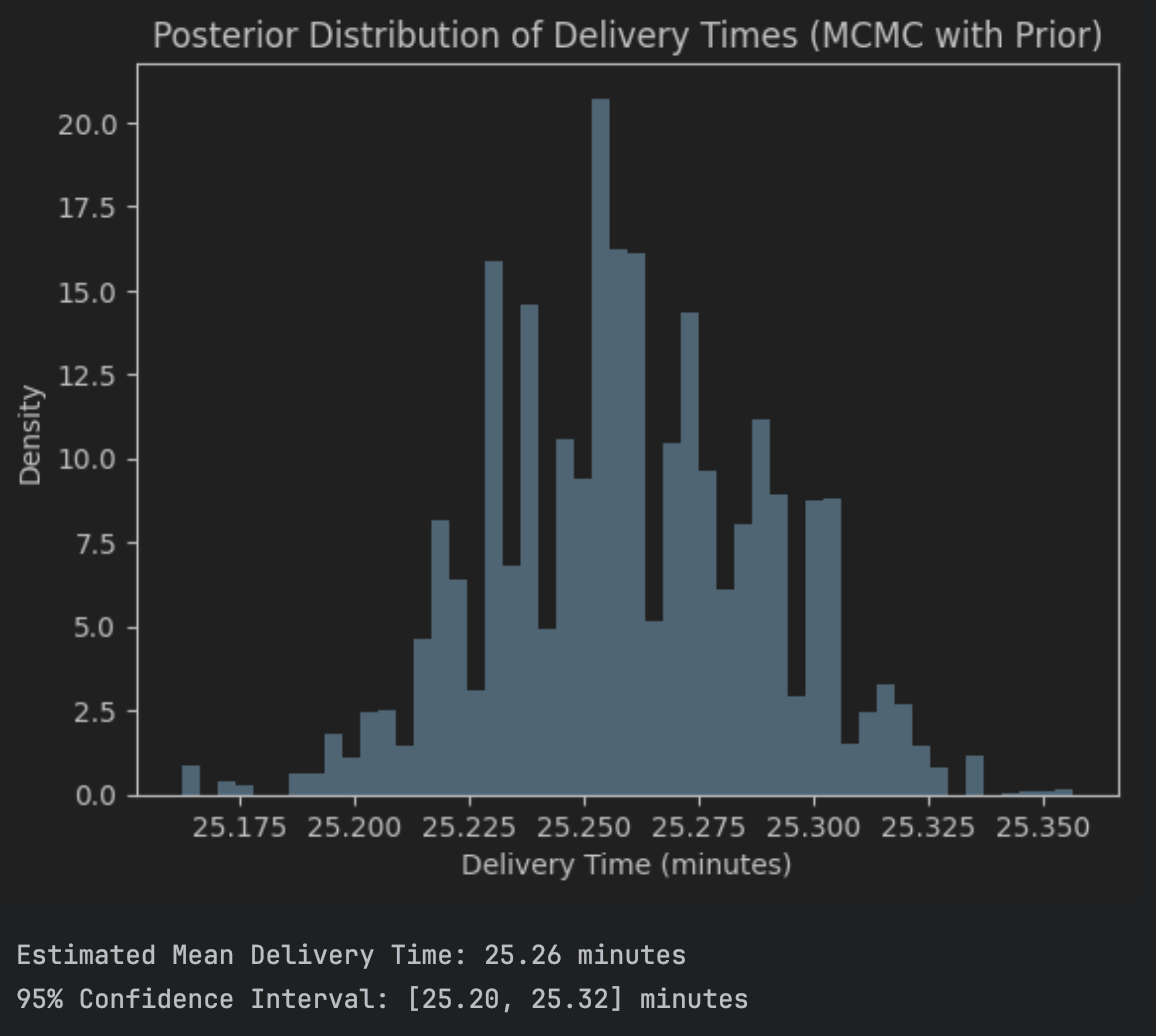
plt.title('Posterior Distribution of Delivery Times (MCMC with Prior)')  
plt.xlabel('Delivery Time (minutes)')  
plt.ylabel('Density')  
plt.show()  
  
# 95% 신뢰 구간 계산  
lower_bound = np.percentile(mcmc_samples, 2.5)  
upper_bound = np.percentile(mcmc_samples, 97.5)  
mean_estimate = np.mean(mcmc_samples)  
  
print(f"Estimated Mean Delivery Time: {mean_estimate:.2f} minutes")  
print(f"95% Confidence Interval: [{lower_bound:.2f}, {upper_bound:.2f}] minutes")