Variational Inference 정리
언제 사용하는가?
- $X = {x_1,x_2,...,x_N}$이 있고 $X$의 Latent Varaible로 $Z$가 있을 때, Posterior인 $P(Z|X)$를 구하고 싶으나 구하기 어려울 때가 있다. 이 때 $p(z|x)$를 Variational Distirbution $q(z)$을 통해서 근사해서 구하는 방식이다.
- 물론 EM(Expectation Maximization Algorithm)을 통해서 Latent Variable $Z$의 분포에 대한 Paraemeter를 구할 수도 있지만, $Z$ 분포의 복잡도로 인해서 실제 진행하기 어려울 수 있어서 대안으로 Variational Inference을 사용한다.
- $p(z|x)$라는 모습에서 유추할 수 있듯이, 우리가 Graphical Model을 사용할 경우 Variataional Inference를 유용하게 쓸 수 있다. Graphical Model은 Node가 Edge로 연결되어 있고 Parent-Child여부 등에 따라서 예측이나 추론 시에 Conditional Distribution을 많이 계산해야 하는데 이 때 유용하다.
이론적 배경
- Kullback-Leibler Divergence은 두 Distribution의 유사도를 구하기 위한 척도로 같으면 0을 다르면 양의 값으로 점차 그 다른 정도에 따라 커지게 된다. 그래서 KL Divergence는 Non-Negative의 특성을 가지고 있다.
- Kullback-Leibler Divergence는 Cross Entrophy - Self Information으로 계산되기 때문에 asymmetric한 특성을 가지고 있다. "Self Information"은 학습과정에서 변하지 않기 때문에 실제로는 Cross Entropy를 최소화하는 것이 Kullback-Leibler Divergence를 최소화하는 것도 동일한 의미를 지닌다.
- KL Divergence을 이용해서 Posterior Distribution과 Variational Distirbution간의 유사도를 구하는 것이다.
- 식으로 쓰면 다음과 같다.
$$q^*(x) = argmin_{q \in Q} D_{KL}(q(z)||p(z|x))$$
$$D_{KL}(q(z)||p(z|x)) = \int q(z) log \frac{q(z)}{p(z|x)} dz$$
$$= \int q(z) log \frac{q(z)p(x)}{p(x|z)p(z)} $$
$$ = \int q(z) log \frac{q(z)}{p(z)}dz + \int q(z) logp(x) dz - \int q(z) log p(x|z) dz$$
$$= D_{KL}(q(z)||p(z)) + logp(x) - E_{z \sim q(z)}[logp(x|z)]$$
- 위와 같이 식을 정리한다고 했을 때 앞서 언급한 바와 같이 KL Divergence는 Non Negative의 성격을 같고 있기 때문에 식을 다음과 같이 정리하고 우항을 ELBO(Evidence Lower BOund)라고 한다. $$0 \le D_{KL}(q(z)||p(z)) + logp(x) - E_{z \sim q(z)}[logp(x|z)]$$ $$ log p(x) \ge E_{z \sim q(z)}[logp(x|z)] - D_{KL}(q(z)||p(z)) $$
- 실제 사용할 때 중요한 부분은 Latent Variable $Z$에 대해서 어떻게 분해를 할 것이며, 어떠한 분포를 따를지 가정하는 것이다. 여기까지 해서 Parameter를 구한 후 EM 알고리즘을 거쳐 모델에 대한 추론작업을 이어갈 수 있게 된다.
- Expectation Maximization Algorithm은 $q(Z) = p(Z|X)$ 일 때 Log Likelihood의 기대값을 최대화한다. 따라서 $D_{KL}[q(Z)||p(Z|X)]$가 0에 가까워져 두 분포가 동일해져서 ELBO값이 최대화된 경우가 EM의 결과라고 볼 수 있다.
- 아래 이미지를 보면 조금 더 쉽게 이해가 될 수 있다.
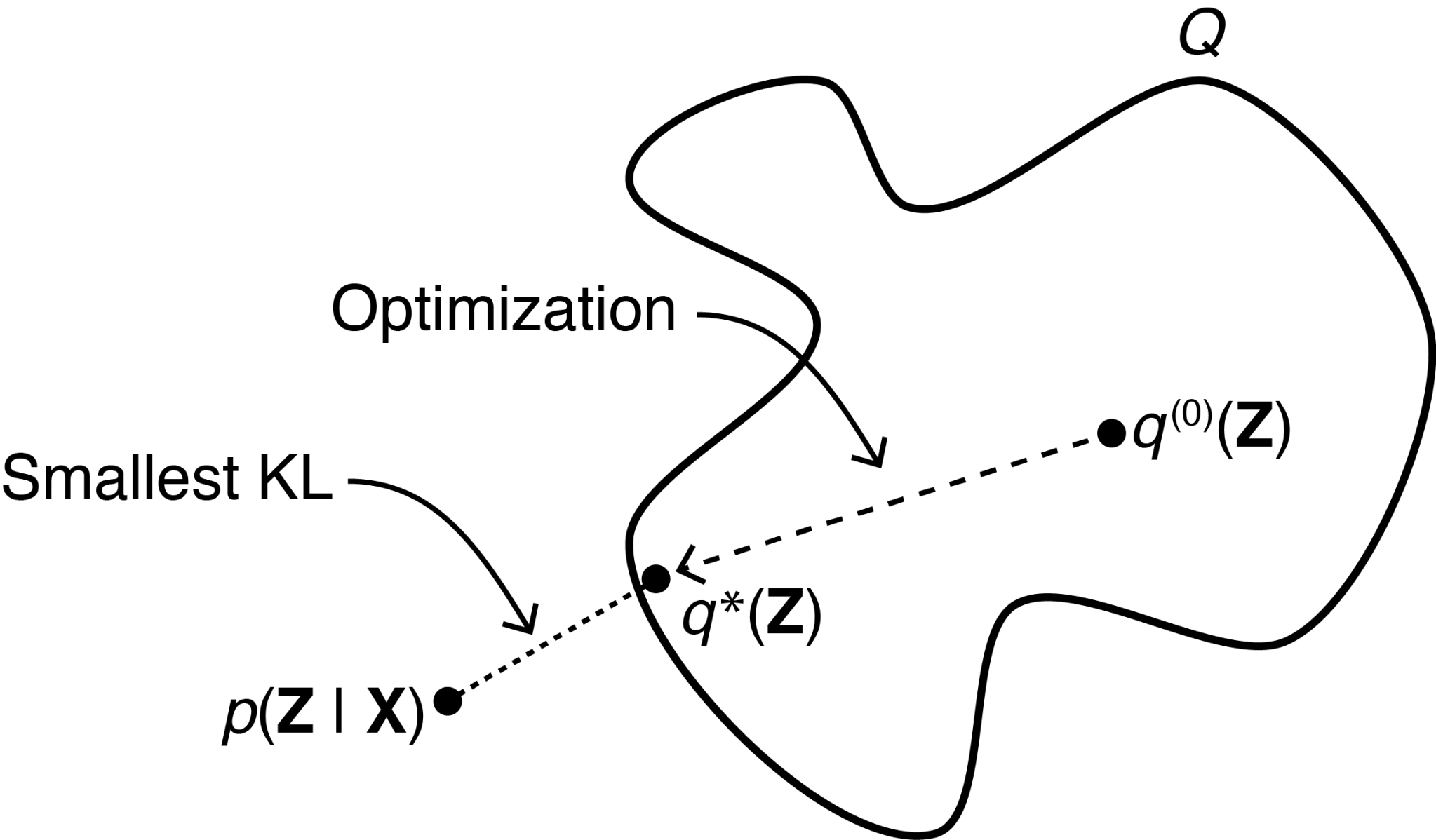
- 이 때 $q(Z)$ 분포의 z는 Mutually Independent하다는 가정을 하고 이러한 분포들을 Mean Field Variational Family라고 한다. 이러한 가정 덕분에 우리는 Distribution $q$ 관련 계산을 할 때 다음처럼 쉽게 Factorization을 활용할 있다. 물론 이로 인해서 Interdependence를 감안하여 계산하기 어렵다라는 단점이 있다. Blei et al. (2017) $$q(\mathbf{z}) = \prod_{j} q_j(z_j)$$
Member discussion