히든마르코프 모델을 이용한 오픈 이온 채널 수 예측(Kaggle - University of Liverpool - Ion Switching Competition)
※ 해당 글은 원 저자은 Gilles Vandewiele 씨의 허락을 받고 번역하였습니다.(링크)
- 저자는 솔루션 코드를 공개하였습니다.(링크)
2 월 24 일, 캐글은 리버풀 대학과 공동으로 25,000 달러의 상금과 함께 새로운 리서치 컴피티션(Research Competition)을 발표했습니다. 이 경쟁에서 우리는 이온 채널(Ion Channel)데이터에 해당하는 전기 신호를 제공 받았으며, 각 시점에서 오픈 채널 수를 자동으로 식별 할 수있는 알고리즘을 만드는 것이 목표였습니다. 처음에는 경쟁이 이국적인 “Quadratic Weighted Cohen Kappa Score (QWK)”로 시작되었지만, 대회가 시작한 지 얼마 되지 않아서 거의 완벽한 결과를 얻었습니다. 얼마 후, 경쟁 지표는보다 합리적인 매크로 F1 스코어(Macro F1 Score)로 바뀌었고 상황이 바뀌게 되었습니다. 저는 몇 가지 이유로 가입하기로 결정했습니다.
- 시계열 데이터입니다.
- 단 하나의 단일 시계열이므로 기능 엔지니어링보다는 전처리 및 모델링에 더 집중할 수 있습니다.
- 데이터는 트레인 세트에서 총 5 백만 회, 테스트 데이터에서 2 백만 회 측정으로 다소 작았습니다. 필요한 총 스토리지는 약 125MB였습니다.
저는 전에 함께 일한 적이있는 가장 머리 좋았던 두 사람(Kha Vo와 Zidmie)과 팀을 이루어 영광을 가졌습니다. 결국 우리는 2600 개 이상이 참여한 대회에서 3 위와 5 천 달러를 확보하였습니다. 1위와 2위는 대회가 끝을 향해 갈 때 비공개 테스트 데이터에서 우리가 발견하지 못했던 데이터 누출을 발견하였습니다.(존재 여부를 알게 된 직후). 다시 말해서 우리 솔루션은 데이터 누출을 활용하지 않은 최고의 솔루션입니다. 최종적으로 우리도 금방 그 데이터 누출을 발견할 수 있었는데 이부분은 우리를 좀 더 실망스럽게 했습니다.

이 블로그 게시물에서는 솔루션에 대한 자세한 개요를 제공하고 솔루션을 구현하는 데 필요한 인사이트를 제공합니다. 아래는 목차입니다.
- 서론
– 문제 정의
– 데이터 훑어보기 & 평가지표 - 전처리
– 전처리 I : 드리프트 제거
– 전처리 II : 선형 변환
– 전처리 III : 전기신호 간섭 제거
– 카테고리 5 = 카테고리 4 + 카테고리 4 - 모델링
– 히든 마르코프 모델 : 1 채널 데이터
– “숨겨진” 히든 마르코프 모델
– 히든 마르코프 모델을 K 채널로 확장
– 히든 마르코프 모델의 메모리 소개 - 사후처리
– Post-processing the posterior probabilities
– A bit of blending - 결론
서론
문제 정의
이온 채널은 동물과 식물에 존재하는 세포막 관통 단백질로서 이온이 채널 구멍을 통과하도록합니다. 학습과 기억을 암호화하고 감염과 싸우고 통증 신호를 활성화하며 근육 수축을 자극합니다. 이 이온 채널은 “패치 클램프 기술”을 통해 기록되고 질병의 특정 특성을 유추하기 위해 분석 될 수 있습니다.

주최자는 다음과 같이 문제를 설명합니다.“이온 채널이 열리면 전류가 흐릅니다. 이러한 상태 변화를 감지하는 기존의 방법은 느리고 힘들다. 인간은 지루한 것 외에도 상당한 편견을 주는 분석을 감독해야합니다. 이러한 어려움은 연구에 사용될 수있는 이온 채널 전류 분석의 양을 제한합니다. 과학자들은 기술이 원시 데이터에서 이온 채널 전류 이벤트를 신속하게 자동 감지 할 수 있기를 희망합니다. 전지의 전기 데이터를 분석하는 기술은 지난 20 년 동안 크게 변하지 않았습니다. 우리가 이온 채널 활동을 더 잘 이해한다면, 연구는 세포 건강 및 이동과 관련된 많은 영역에 영향을 줄 수 있습니다. 인간의 질병에서부터 기후 변화가 식물에 미치는 영향에 이르기까지, 이온 채널의 빠른 탐지는 주요 세계 문제에 대한 솔루션을 크게 가속화시킬 수 있습니다.”

데이터 훑어보기 & 평가지표
우리에게 제공되는 데이터는 다소 단순하며, 이는 이번 대회에서 좋은 점 중 하나입니다. 데이터에는 세 개의 컬럼만 포함됩니다.
타임 스탬프(Timestamp)
각 타임 스탬프에 대한 암페어 값 (전류). 이 값들은 10kHz의 샘플링 주파수에서 측정되었습니다.
해당 타임 스탬프에 해당하는 오픈 채널 수입니다 (트레인 데이터에만 제공됨).
트레인 데이터 세트는 5 백만 행으로 구성되는 반면 테스트 데이터 세트는 2 백만 행으로 구성됩니다. 경쟁의 목표는 2 백만 행에서 매크로 F1 스코어(Macro F1 Score)를 최대화하는 것입니다. 특정 클래스의 F1 Score는 정밀도 및 리콜의 조화평균으로 정의됩니다.

“매크로”F1은 단순히 클래스 당 평균 F1 스코어입니다. 따라서 K 클래스가 있다면 K F1 점수를 계산 한 다음 K 점수의 평균을 구합니다. 제공된 데이터를 검사하면 이미 몇 가지 흥미로운 결론을 내릴 수 있습니다.

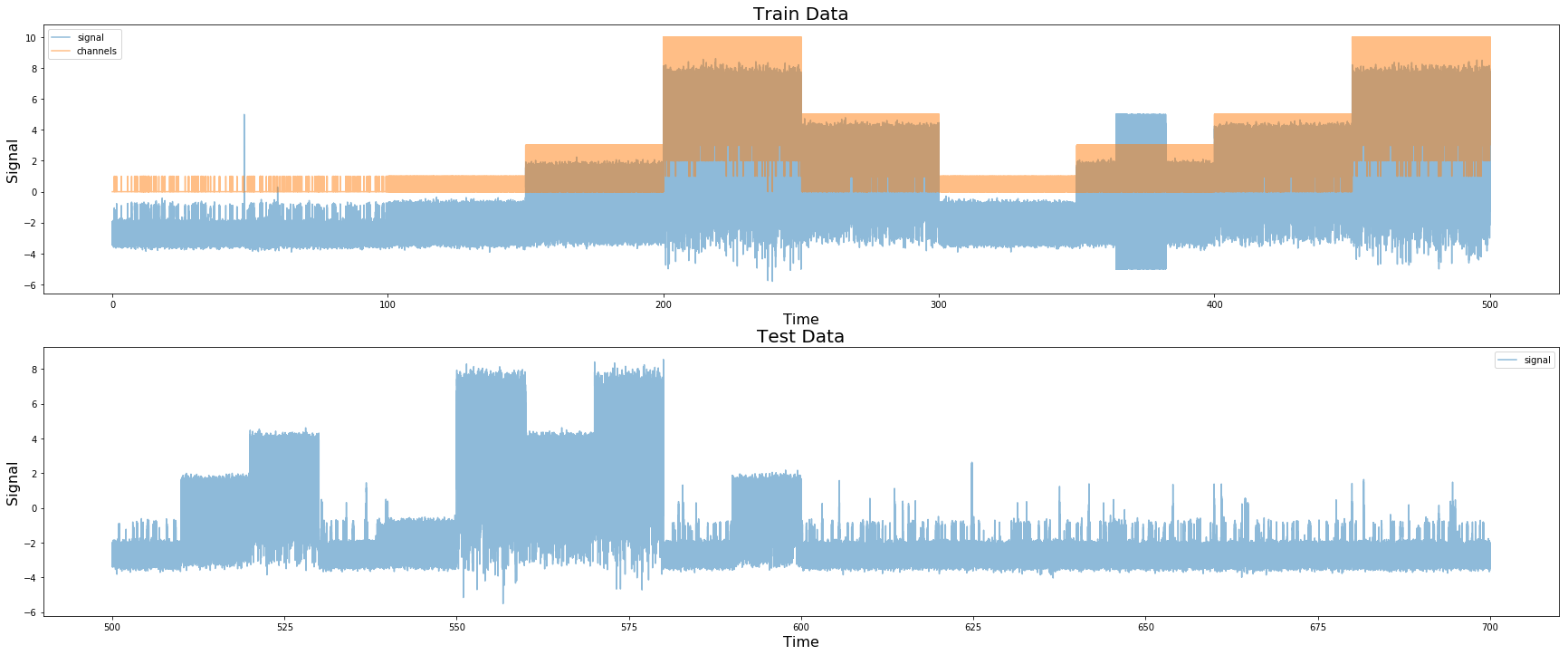
제공된 원본 데이터 (트레인 및 테스트)
먼저 테스트 데이터에서 오픈 채널을 검사하여 데이터가 500K 측정 단위로 구성되어 있음을 알 수 있습니다. 전기 신호에서도 이러한 전이를 일괄 적으로 볼 수 있습니다. 테스트 세트에서 100K의 배치를 찾을 수 있습니다. 또한 트레인 세트에서 500K의 배치는 실제로 10 x 500K 배치로 구성됩니다.

트레이닝 데이터는 500K의 여러 배치로 구성됩니다.(One Feature Model by Chris Deotte)
트레이닝 세트에서 오픈 채널을 더 검사하면 트레이닝 세트에서 5 개의 다른 그룹을 찾을 수 있습니다.
- 오픈 채널이 0 또는 1 인 그룹입니다. 0과 1이 많은 그룹입니다. (카테고리 1)
- 오픈 채널이 0 또는 1 인 그룹입니다. 많은 1, 소수 0입니다. (카테고리 2)
- 0, 1, 2, 3에 해당하는 오픈 채널 그룹 (카테고리 3)
- 0, 1, 2, 3, 4, 5에 해당하는 오픈 채널 그룹. (카테고리 4)
- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10과 동일한 오픈 채널 그룹. (카테고리 5)
- 놀랍게도 테스트 데이터에는 카테고리 1과 매우 유사한 데이터가 많았지만 트레인 데이터에는 나타나지 않는 전기 신호에 약간의 스파이크가있었습니다. 따라서 우리는 이것을 별도의 카테고리로 분류합니다 (카테고리 6).
이러한 인사이트를 평가지표와 결합 할 때, 최대 10 개의 오픈 채널(Open Channel)을 가진 그룹 (카테고리 5)이 매크로 F1 평균에 가장 큰 영향을 미치게됩니다. 다른 그룹에는 나타나지 않는 5 개의 고유 한 클래스 (6, 7, 8, 9, 10)가 있으므로이 데이터 그룹은 매크로 F1 점수에 50 % 이상 기여합니다. 경쟁 과정에서“Waylon Wu는 확인 해본 결과 공개 LB가 처음 30 % (또는 600000)의 테스트 값으로 구성되었고 개인 LB가 나머지 70 % (1400000)로 구성되어 있음을 발견했습니다.
전처리
전처리 I : 드리프트 제거
우리는 트레인 데이터의 신호의 시작과 끝에 그리고 테스트 신호의 다른 곳에 이상한 드리프트가 있음을 발견했습니다… 우리는 곡선 드리프트 (예 : 트레인 데이터 신호의 끝)와 선형 드리프트의 두 가지 유형의 드리프트를 발견했습니다. (예를 들어, 트레인 데이터 신호의 시작에서, 시간 = 50 정도).

신호에서 두 가지 유형의 드리프트를 나타내는 두 개의 서브 샘플.결국, “선형”드리프트는 전혀 선형이 아니라 실제로 “곡선”드리프트의 작은 부분이었습니다 (예 : 곡선 드리프트의 전반도 선형으로 보입니다). 경쟁이 시작된 직후, 이은호와 Markus F는 경쟁 주최측이 매우 낮은 주파수의 사인 함수 (1.000.000 값)를 사용하여 데이터에 인공 소음을 발생 시켰음을 발견했습니다. Chris Deotte는 두 개의 독립적 인 분석에서 얻은 통찰력을 정리하여 가장 깨끗한 드리프트 제거를 수행하고 다른 모든 경쟁 업체에서 사용할 수있는 데이터 세트를 만들었습니다 (Chris 감사합니다). 새로운 데이터는 다음과 같습니다.드리프트 제거 후 데이터time = 360에서 time = 390까지 무언가 잘못되고 있음을 알 수 있습니다. 우리는 이러한 문제가 테스트 세트에 존재하지 않았기 때문에 이에 대해 신경 쓰지 않기로 결정했으며 트레인 세트에서 이 데이터를 제거했습니다.
전처리 II : 선형 변환
데이터를 검사함으로써, 트레인 데이터 신호와 오픈 채널의 수가 서로 밀접하게 관련되어 있음이 분명해집니다. 실제로 전기 신호에 선형 변환을 적용한 다음 결과 값을 반올림하면 이미 성능이 우수합니다.

전기 신호와 오픈 채널 수는 서로 밀접하게 관련되어 있습니다.
우리는 전기 신호 값을 오픈 채널 수에 가장 잘 매핑하는 데이터 카테고리 별로 선형 변환을 배우기로 결정했으며, 이는 향후 단계에서 더 쉽게 분석 할 수있게했습니다. 변형은 다소 간단합니다. 다음 함수 (1D 선형 회귀)에 대해 서로 다른 두 가지 매개 변수를 배웠습니다.
전기 신호 (x)를 각각의 오픈 채널 수에 더 잘 맞추기위한 1D 선형 회귀. o는 오프셋이고 s는 선형 회귀의 기울기입니다.
우리의 기울기는 각 카테고리 (0.8107)에 대해 동일했으며 오프셋은 카테고리에 따라 다릅니다 (카테고리 2, 3, 4 및 6의 경우 2.221318; 카테고리 5의 경우 4.4288541, 카테고리 1의 경우 2.180783).

정렬 된 데이터 전기 신호가 이제 각각의 오픈 채널 수와 매우 잘 일치하는지 확인하십시오. 신호 값을 반올림하면 이미 강력한 베이스라인이 됩니다.
이 부분을 설명하기 위한 파이썬 코드를 제공하고 있으니 클릭하셔서 확인할 수 있습니다.
전처리 III : 전기신호 간섭 제거
이전 섹션에서 언급했듯이 정렬 된 전기 신호 값을 반올림하면 이미 강력한 베이스라인이 됩니다. 불행히도, 그것은 완벽한 점수를 얻지 못할 것입니다… 그것은 우리의 데이터 셋에 노이즈가 존재하기 때문입니다 (운좋게도, 이것은 아주 사소한문제일 수 있었습니다)! 다음을 간단히 계산하여이 노이즈를 검사 할 수 있습니다.
아래는 트레인 세트의 첫 10000 노이즈 값의 플롯입니다.

트레이닝 세트의 첫 10000 노이즈 값
눈으로는보기 어려울 수 있지만, 노이즈 안에는 약간의 물결 무늬가 있습니다. 중앙 창 크기가 50 인 이동 평균을 취하면 더욱 분명해집니다.

10000 노이즈 값의 이동 평균 (크기 50의 Centerd Window).
평균 200 개 값마다 피크가있는 웨이브를 명확하게 볼 수 있습니다. 주기가 약 200kHz 인 10kHz의 샘플링 주파수에서 측정 된주기 신호는 50Hz의 주파수에 해당합니다. 영국의 AC 전원 (경쟁은 Uni of Liverpool에 의한)의 주파수가 50Hz라는 것이 밝혀졌습니다! 노이즈에서이 패턴을 제거하기 위해 100000 개의 노이즈 값의 각 배치에 사인 함수를 맞추기로 결정했습니다 (scipy.optimize를 사용할 수 있음).
대역 통과 및 대역 저지 필터와 같은 신호 처리 기술로도이를 수행 할 수 있지만 간단한 사인 함수로 더 나은 결과를 얻을 수 있습니다. 또한 사인 함수에 여러 구성 요소가있는 것 (즉, 진폭, 위상 및 주파수가 다른 여러 사인파)이 가장 효과적이라는 것이 밝혀졌습니다.

10000 개의 노이즈 값과 해당하는 사인 함수.
카테고리 5 = 카테고리 4 + 카테고리 4
우리의 노이즈 제거 기술은 하나를 제외하고 모든 카테고리에서 실제로 잘 작동하는 것 같았습니다. 카테고리 5의 데이터에는 다른 모든 것과 구별되는 고유 한 것이 있습니다. 실험을 통해 카테고리 4에서 두 개의 임의 배치를 함께 추가하여 카테고리 5의 데이터를 매우 잘 모방 할 수 있음을 알았습니다.

카테고리 4의 두 배치를 함께 추가하여 카테고리 5의 합성 데이터 생성
이 가정을 함으로써 cat 5의 잡음이 두 개의 사인 함수를 추가한다고 가정 할 수 있습니다. 또한, 이러한 통찰력은 예를 들어 신경망에 유용 할 수있는 데이터 확대를 허용한다.
결과적으로 이 인사이트는 실제로 누출과 관련된 것이었습니다. 우리는이 길을 충분히 오랫동안 추구하지는 않았지만, 개인 테스트 데이터는 정확히 두 가지 카테고리 4 배치의 합이었습니다. 그 중 하나는 트레인 세트에서 찾을 수 있습니다…
경쟁 후 팀 동료 인 지디 미가 발견했습니다 (일부). 이 누출을 파악하는데 약 30 분 정도 소요됩니다 (개인 점수를 0.95430으로 개선). 2 개월의 업무보다 누출로 인해 30 분 만에 모델이 훨씬 개선되었다는 것을 알고 약간 실망했습니다. 나중에 그는 전체 누출을 발견했습니다. y_test [570000 : 5800000] = predict (X_test [5700000 : 5800000]-X_train [4000000 : 4100000]) + y_train [4000000 : 4100000]. 이제 카테고리 4 데이터 (최대 5 개 채널)를 예측하므로 훨씬 쉬운 작업이됩니다.

모델링
히든 마르코프 모델 : 1 채널 데이터

이 밈은 사용할 필요가 없었습니다. 결국, 개인 테스트 데이터의 누출이 실제 승자 인 것으로 판명되었기에… (아마도 새로운 밈을 만들어야합니다…).
히든 마르코프 모델 (Hidden Markov Models)과 같은 순차적인 상태 공간 모델은 이러한 유형의 문제에서 오랫동안 최첨단 기술이었습니다. 최근에는 딥 러닝 변형이 제안되었습니다 (예 : 대회 주최자의 논문을 참조). 모든 인공적인 요소를 제거하기 위해 데이터를 사전 처리하고 있기 때문에이 경쟁에서 모델링 기법 인 히든 마르코프 모델로 가기로 결정했습니다.
숨겨진 마르코프 모델에 대한 훌륭한 소개가 많이 있으므로 여기서 자세히 설명하지 않겠습니다. 우리가 알아야 할 것은 각각의 숨겨진 마르코프 모델에 속하는 다른 매개 변수가 있다는 것입니다.
- 숨겨진 상태의 수 (= K)
- 초기화 확률 (크기 K의 벡터)
- 전이 행렬 (K x K 행렬)
- 출력 확률. 각각의 숨겨진 상태는 특정 관찰 가능 값을 방출합니다. 이러한 출력확률은 불연속 출력에 대한 다항식과 연속 출력에 대한 가우시안 (전기 신호가 연속적이므로 여기서 사용할 것)과 같이 서로 다른 분포를 가질 수 있습니다.
요컨대, 오픈 채널 (숨겨진 변수)은 특정 마르코프 프로세스(Markov Process)를 따르고 전이 행렬에 의해 결정되는 특정 확률로 한 값에서 다른 값으로 이동합니다. 마르코프 프로세스가 특정 숨겨진 (hidden) 상태에 있는 경우 여기에서 전기 신호로 관찰 가능한 값을 방출합니다.
예를 들어, 이진 반응 변수 (오픈 채널 = 0 또는 1)가있는 카테고리 2에 중점을두고 마르코프 모델에 2 개의 숨겨진 상태가 있다고 가정합니다. 오픈 채널의 수가 0과 같을 때의 숨겨진 상태와 1과 같을 때의 하나의 숨겨진 상태가 있을 것입니다. 우리는 여기서 트레인데이터(예: 특정 상태에서 다른 상태로 전이하는 횟수를 세보거나 특정 오픈채널의 수에 대응하는 신호를 보는 식)를 확인해서 쉽게 전이행렬과 출력에 대한 분포를 확인할 수 있습니다.

교육 데이터의 카테고리 2에 대한 추정 가우시안 및 전이 확률.
즉, 예를 들어 오픈 채널 수가 1과 같으면 신호 값도 약 1이됩니다 (비트 차이가 있음). 다음 값은 93.6 %의 확률로 1이 되고 6.4 %의 확률로 0 입니다. 위의 그림과 같이 트레인 데이터를 사용하여 Baum-Welch 알고리즘을 적용하여 이러한 파라미터를 추정 할 수 있습니다. 이 알고리즘은 “비지도 학습인”인 Expectation-Maximization 알고리즘의 특별한 경우입니다 (더 빠른 반복을 허용하는 교차 검증이 필요하지 않음). 간단히 말해서 (그리고 간단한 방법으로) 초기 매개 변수를 기반으로 예측을 한 다음 이러한 예측을 사용하여 수렴 할 때까지 매개 변수를 업데이트합니다. 매개 변수가 학습되면 다음 두 알고리즘 중 하나를 적용하여 추론을 수행 할 수 있습니다.
- Viterbi Algorithm — 가장 가능성이 높은 시퀀스를 반환합니다
- Forward-Backward Algorithm (또는 Maximum A Posteriori) — TxK 확률 행렬 P를 반환합니다. p[t][k]는 t시점에 히든 상태에 있을 확률 p에 대한 값이다.
초기 테스트는 이미 포워드-백워드 알고리즘(Forward-Backward Algorithm)이 Viterbi보다 약간 더 우수하지만 느리게 작동하는 것으로 나타났습니다. 이 알고리즘은 Baum-Welch 알고리즘에서도 사용됩니다. 파이썬에서이 모든 알고리즘을 적용하는 훌륭한 라이브러리는 hmmlearn입니다.
카테고리 2의 사전 처리 된 데이터에 2 단계 HMM을 적용 해 보겠습니다.
# 2-state HMM
sub_signal = <PREPROCESSED SIGNAL CATEGORY 2>
sub_channels = <CATEGORY 2 LABELS>
def markov_p_trans(states):
# https://www.kaggle.com/friedchips/the-viterbi-algorithm-a-complete-solution
max_state = np.max(states)
states_next = np.roll(states, -1)
matrix = []
for i in range(max_state + 1):
current_row = np.histogram(states_next[states == i], bins=np.arange(max_state + 2))[0]
if np.sum(current_row) == 0: # if a state doesn't appear in states...
current_row = np.ones(max_state + 1) / (max_state + 1) # ...use uniform probability
else:
current_row = current_row / np.sum(current_row) # normalize to 1
matrix.append(current_row)
return np.array(matrix)
# Estimate the transition matrix based on the ground truth
Ptran = markov_p_trans(sub_channels)
# Estimate means and covs per unique ground truth value
means = []
covs = []
for c in [0, 1]:
means.append(np.mean(sub_signal[sub_channels == c]))
covs.append(np.cov(sub_signal[sub_channels == c]))
# Defining our HMM
hmm = GaussianHMM(
n_components=2, # Number of hidden states
n_iter=50, # Total number of iterations
verbose=True, # Show logs
algorithm='map', # Use maximum a posteriori instead of Viterbi
params='stmc', # Optimize start probs, transmat, means, covs
random_state=42,
init_params='s', # Manually initialize all but start probabilities
covariance_type='full', # Separate covariance per hidden state
tol=0.01 # Convergence criterion
)
# Initialize the parameters of our HMM
hmm.n_features = 1
hmm.means_ = np.array(means).reshape(-1 ,1)
hmm.covars_ = np.array(covs).reshape(-1, 1, 1)
hmm.transmat_ = Ptran
# Fit our HMM
hmm.fit(sub_signal.reshape(-1, 1), lengths=[100000]*10)
# Make predictions
preds = hmm.predict(sub_signal.reshape(-1, 1), lengths=[100000]*10)
# Calculate our F1 score on this category of data
print(f1_score(sub_channels, preds, average='macro'))
숨겨진 상태가 2개인 숨겨진 마르코프 모델을 생성하면 학습 데이터를 기반으로 출력 분포 및 전이 행렬의 매개 변수를 추정합니다. Marco가 올바르게 지적했듯이“길이 = [100000] * 10”은 카테고리 2의 데이터 배치가 2 개라는 사실에서 비롯됩니다. 각 배치의 길이는 500K이고 다시 5 개의 배치로 100K입니다. 따라서 총 10 만 개의 시퀀스가 있습니다.

스크립트 출력 hmmlearn 라이브러리는 5 개의 반복에 대해 Baum-Welch 알고리즘을 수행하여 매개 변수를 조정 한 후 수렴합니다. 이 데이터 카테고리에서 F1 점수는 0.9961과 같습니다.
따라서이 간단한 방법을 사용하면 데이터의 카테고리 2에서 F1 점수 0.9961을 이미 달성 할 수 있습니다. 데이터의 카테고리 1과 2는 거의 완벽한 성능을 가진 가장 쉬운 데이터입니다. F1 점수는 최대 오픈 채널 수에 따라 빠르게 떨어집니다. 예를 들어, 데이터의 카테고리 5에서 F1 점수가 0.9에 도달 할 수 없습니다.
“숨겨진” 히든 마르코프 모델
주최자가 출판 한 논문을 읽을 때 오픈 채널 수가 마르코비안 프로세스를 따르는 동안 숨겨진 마르코프 모델에 의해 생성된다는 것이 분명해졌습니다.

실제 값은 (오픈 채널)은 마르코프 프로세스에 의해 생성되며, 이는 합성 (이 대회의 경우) 또는 실제 (실제 이온 채널이 마르코프 프로세스를 따른다고 가정)에 의해 생성 될 수 있습니다. 이 접지 진실은 패치 클램프 앰프를 통해 재생되고 기록되어 노이즈가있는 관측 가능한 데이터 (전기 신호)를 생성했습니다(주최자의 글에서 발췌)
이 숨겨진 마르코프 모델은 고유 한 오픈 채널 값의 수보다 더 많은 숨겨진 상태로 구성됩니다. 이것은 Markus F가 대회 기간 중 언급하였습니다.

왼쪽에 “vanilla”HMM이 있고 오른쪽에 2 계층 또는 숨겨진 숨겨진 마르코프 모델.
이에 접근하는 간단한 방법은 2 계층 모델에서 중간 계층 (y (t))을 무시하는 것입니다. 따라서 우리는 고유한 오픈 채널 수보다 더 많은 숨겨진 상태를 가진 숨겨진 마르코비안 프로세스를 가지고 있습니다 (예 : 2 개의 가능한 오픈 채널 값에 대해 5 개의 숨겨진 상태). 이 통찰력을 카테고리 2 데이터에 적용 해 보겠습니다. HMM에서 4 개의 숨겨진 상태를 사용합니다 (다른 숫자를 실험했지만 4가 가장 효과적 임). 처음 두 개의 숨겨진 상태는 오픈 채널 수가 1 일 때에 해당하고 다음의 두 가지 숨겨진 상태는 오픈 채널이 0 일 때에 해당합니다. 초기 전환 매트릭스를 추정하는 것은 이제 우리가 직접 예측할 수 없으므로 더욱 어려워집니다. 트레인 데이터, 우리는 전이 행렬을 수동으로 조정했습니다.
# 4-state HMM
sub_signal = <PREPROCESSED SIGNAL CATEGORY 2>
sub_channels = <CATEGORY 2 LABELS>
# Estimate the transition matrix based on the ground truth
Ptran = [[0.9879, 0.0121, 0 , 0 ],
[0.0424, 0.6709, 0.2766, 0.0101],
[0 , 0.2588, 0.7412, 0 ],
[0 , 0.0239, 0 , 0.9761]]
# Estimate means and covs per unique ground truth value
means = []
covs = []
for c in [0, 1]:
means.append(np.mean(sub_signal[sub_channels == c]))
covs.append(np.cov(sub_signal[sub_channels == c]))
means = [means[1], means[1], means[0], means[0]]
covs = [covs[1], covs[1], covs[0], covs[0]]
# Defining our HMM
hmm = GaussianHMM(
n_components=4, # Number of hidden states
n_iter=50, # Total number of iterations
verbose=True, # Show logs
algorithm='map', # Use maximum a posteriori instead of Viterbi
params='stmc', # Optimize start probs, transmat, means, covs
random_state=42,
init_params='s', # Manually initialize all but start probabilities
covariance_type='full', # Separate covariance per hidden state
tol=0.01 # Convergence criterion
)
# Initialize the parameters of our HMM
hmm.n_features = 1
hmm.means_ = np.array(means).reshape(-1 ,1)
hmm.covars_ = np.array(covs).reshape(-1, 1, 1)
hmm.transmat_ = Ptran
# Fit our HMM
hmm.fit(sub_signal.reshape(-1, 1), lengths=[100000]*10)
# Make predictions
preds = hmm.predict(sub_signal.reshape(-1, 1), lengths=[100000]*10)
preds = list(map(lambda x: {0: 1, 1: 1, 2: 0, 3: 0}[x], preds))
# Calculate our F1 score on this category of data
print(f1_score(sub_channels, preds, average='macro'))4 상태 HMM을 맞추기 위해 전이 행렬을 수동으로 초기화하고 다른 숨겨진 상태에 대한 평균과 공분산을 재사용합니다.

스크립트 출력내용 일부로 hmmlearn이 반복수행 중 출력하는 음의 로그가능도가 2개의 숨겨진 상태를 갖는 로그 가능도의 두배만큼 큰 것에 주목할 필요가 있습니다.
알 수 있듯이 우리는 이제 0.9972의 F1 점수를 얻습니다. 이는 2 개의 숨겨진 상태만 사용하는 것과 비교하여 대략 0.001의 증가입니다. 이 개선은 특히 오픈 채널 수가 많을수록이 개선이 더 많이 된다는 사실을 고려하면 매우 중요합니다. F1 점수에서 0.001의 차이는 결국 은메달과 금메달의 차이입니다. F1은 더 많은 숨겨진 상태를 도입하거나 초기 전이 매트릭스를 조정하여 훨씬 더 향상 될 수 있지만, 전이 행렬이 작을수록 몇 가지 장점이 있었으므로 나중에 더 명확 해집니다. 관련된 파이썬 코드는 여기서 확인할 수 있습니다. 그리고 몇몇 정보에 대해서는 우리가 어떻게 수작업으로 전이행렬을 조정했지는 이 노트북을 참고하시면 됩니다.
히든 마르코프 모델을 K 채널로 확장
최대 1 개의 오픈 채널이있는 데이터의 카테고리 1과 2를 매우 정확하게 모델링 할 수있는 것 같습니다. 문제는 (25,000 달러) 이제 이 접근 방식을 하나 이상의 오픈 채널을 사용하여 데이터의 다른 카테고리 에 적용 할 수 있는지 여부입니다. 이것은 간단한 문제가 아닙니다. 큰 초기 전이행렬을 설계하고 어떤 숨겨진 상태가 어떤 오픈 채널 숫자와 대응하는지를 결정하는 것은 힘들고 비싼 작업입니다.) (실제로는 검색 공간이 무한대로 크기 때문에).
따라서, 우리는 하나의 배치에서 오픈 채널의 최대수를 K라고 할 때 K개의 독립적 인 바이너리 마르코비안 프로세스를 처리한다고 가정했다. 또한 이러한 마르코비안 프로세스 각각은 데이터의 카테고리 2와 매우 유사한 매개 변수를 갖습니다. 여러 개의 독립적 인 숨겨진 프로세스가있어 관측 가능한 변수를 생성하는 것은 팩토리 히든 마르코프 모델에 적합합니다. 불행히도, 우리는 파이썬에서 좋은 라이브러리를 찾지 못했습니다 ( ‘factorialHMM’은 있지만 작동하지 않고 ‘Pyro.ai’는 있지만 학습 곡선은 매우 가파 릅니다 (적어도 나에게는)).
구현이 없었기 때문에 우리는 이것을 직접 구현하는 것이 어렵고 긴 과정이라는 것을 깨달았습니다. 따라서 데이터를 최대 1 개의 오픈 채널로 모델링하는 데 사용되는 더 작은 전이 행렬을 더 큰 전이 행렬로 변환함으로써 독립적 인 프로세스 측면에서“해킹”하기로 결정했습니다. 새로운 대형 마르코프 프로세스에서 숨겨진 상태는 각각 독립 프로세스에서 가능한 숨겨진 상태 조합에 해당합니다. 순서는 중요하지 않습니다 (즉, (0, 2) (1 프로세스는 숨겨진 상태 0에 있고 다른 프로세스는 숨겨진 상태 2에 있음)는 (2, 0)와 동일합니다). 이 구성은 아래 그림과 같이 재귀 적으로 수행됩니다.

2 개의 독립적 인 프로세스를 모델링하기 위해 먼저 숨겨진 상태의 모든 가능한 조합을 캡처하는 4 개의 숨겨진 상태를 16 개의 숨겨진 상태로 확장합니다. 그런 다음 유사한 상태를 함께 그룹화합니다 (동일한 색상으로 표시). 그런 다음 새로운 10×10 매트릭스를 40×40으로 확장하고 다시 20×20으로 축소하여 3 개의 프로세스를 계속 모델링 할 수 있습니다. 마르코프 체인의 모든 상태들 사이에는 전이가 있습니다 (모두 그리지 않았습니다).

독립적 인 프로세스를 모델링하기 위해 4×4 전이 매트릭스 확장
각 반복에서 먼저 전이 행렬을 확장합니다. 초기 전이 행렬이 N x N 인 경우, 새로 확장 된 행렬은 N 개의 초기 상태와 가능한 새로운 K 개의 상태와의 모든 가능한 상호 작용을 캡처하는 N * K x N * K입니다. 2 개의 독립적 인 프로세스가있는 경우 프로세스 1은 숨겨진 상태 0에 있고 프로세스 2는 숨겨진 상태 1에 있습니다.이 확장 후 유사한 상태 (예 : 그림의 녹색 셀)를 그룹화합니다. 이 예제를 사용하면 프로세스 1은 숨겨진 상태 0에 있고 프로세스 2는 숨겨진 상태 1에있는 프로세스 1은 프로세스 1은 숨겨진 상태 1에 있고 프로세스 2는 숨겨진 상태 0에 있습니다. 새로 생성 된 행렬의 크기는 C x C입니다. K는 가능한 상태로부터 P 개의 독립적 인 프로세스로부터 반복과의 조합의 수와 동일하다. 예를 들어, 4 개의 숨겨진 상태와 3 개의 독립적 인 프로세스에서 C는 20과 같습니다 (Comb_with_Repetition (4, 3) = Comb (4 + 3 – 1, 3) = 20).
다음은 이를 수행하는 Python 코드입니다.
def calculate_matrix(transition_matrix, states, number_processes):
# Fill in diagonals such that each row sums to 1
for i in range(transition_matrix.shape[0]):
transition_matrix[i, i] = 1 - np.sum(transition_matrix[i, :])
n0 = len(states)
new_transition_matrix = transition_matrix.copy()
new_states = [(x,) for x in range(n0)]
for process in range(1, number_processes):
# We expand our current transition matrix (that models up to `process` number
# of separate processes) its' dimensions by n0. We basically add another
# possible state transition for a new process.
nc = new_transition_matrix.shape[0]
temp_transition_matrix = np.zeros((n0*nc, n0*nc))
temp_states = []
for i in range(n0):
temp_states.extend([s + (i,) for s in new_states])
for j in range(n0):
# We add i -> j as our final transition
temp_transition_matrix[i*nc:(i+1)*nc, j*nc:(j+1)*nc] = transition_matrix[i][j] * new_transition_matrix
# We now group similar processes together to reduce our matrix.
# E.g. (1, 2, 3) is the same as (2, 3, 1)
new_states = sorted(list(set([tuple(sorted(x)) for x in temp_states])))
new_transition_matrix = np.zeros((len(new_states), len(new_states)))
for i in range(len(new_states)):
ix_i = [k for k, x in enumerate(temp_states) if tuple(sorted(x)) == new_states[i]]
for j in range(len(new_states)):
ix_j = [k for k, x in enumerate(temp_states) if tuple(sorted(x)) == new_states[j]]
new_transition_matrix[i, j] = np.sum(temp_transition_matrix[ix_i, :][:, ix_j])
new_transition_matrix[i, j] /= len(ix_i)
new_channels = []
for s in new_states:
new_channels.append(sum([states[x] for x in s]))
new_channels= np.array(new_channels)
return new_transition_matrix, new_channels이 알고리즘은 구현하기가 쉽지 않았으며 간단한 (그러나 훨씬 더 읽기 쉬운) 구현으로 인해 프로세스 수가 10 일 때 몇 주 동안 예상 런타임이 발생했습니다. 4×4 초기 행렬로 10 개의 프로세스로 전이 행렬을 생성하는 데 약 2 분이 걸리고 5×5 행렬의 경우 훨씬 더 길어집니다 (따라서 우리는 4×4를 유지했습니다).
히든 마르코프 모델의 메모리 소개
우리는 전진 후진 알고리즘을 직접 구현하여 많은 자유를 얻었습니다. 우리는 알고리즘의 바닐라 구현에 대해 많은 다른 조정을 시도했지만 가장 중요한 개선은 메모리 도입이었습니다. 역방향 패스에서 타임 스텝 t에서 확률을 계산할 때 순방향 패스에서 타임 스텝 t에서 계산 된 확률을 사용합니다.
역 확률 (베타) 계산 Psig는 출력 확률, Ptran 전환 확률, c 계수입니다 (높을수록 순방향 확률에 더 큰 영향을 미침).
순방향 확률 (알파) 계산.
총 3 회의 패스를 실시합니다. 하나의 정방향 패스. 다음 정방향 패스에서 알파를 사용하고 마지막으로 새로 계산 된 베타를 사용하여 마지막 정방향 패스를 사용합니다. Psig는 다음과 같이 계산됩니다.
Psig 계산은 평균 0의 가우시안 분포와 조정 가능한 시그마를 사용합니다.
def forward(Psig, Ptran, etat_in=None, coef=1, normalize=True):
if etat_in is None:
etat_in = np.ones(Psig.shape)/Psig.shape[1]
alpha = np.zeros(Psig.shape) # len(sig) x n_state
etat = np.zeros(Psig.shape) # len(sig) x n_state
C = np.zeros(Psig.shape[0]) # scale vector for each timestep
etat[0] = etat_in[0]
alpha[0] = etat_in[0]
if normalize:
alpha[0] = etat_in[0]*Psig[0]
alpha[0]/=alpha[0].sum()
for j in range(1, Psig.shape[0]):
etat[j] = alpha[j-1]@Ptran
if normalize:
etat[j] /= etat[j].sum()
etat[j] = (etat[j]**coef) * ((etat_in[j])**(1-coef))
if normalize:
etat[j] /= etat[j].sum()
alpha[j] = etat[j] * Psig[j]
alpha[j] /= alpha[j].sum()
return alpha, etat순방향 및 역방향 패스에 모두 사용 된 조정 된 기능입니다. 역방향 패스의 경우 전이 행렬을 조옮김하고 신호를 반전 시켰습니다.
후 처리
사후 확률 후 처리
우리의 전진 후진 알고리즘을 을 한 후에, 우리는 각각의 숨겨진 상태와 각 시간 단계에 대한 확률과 함께 “TxK”를 남겼습니다. 동일한 오픈 채널 값에 해당하는 여러 개의 숨겨진 상태가 있으므로 이러한 확률을 예측으로 변환하려면 다른 사후 처리 단계가 필요합니다. 첫 단계로, 우리는 timeK 상태를 이용하여 asK 확률의 내적을 가중 합계와 같고 따라서 지속적인 가치 Y를 얻었으며, 각 클래스와 각 임계 값을 배우기로 결정했습니다. 데이터 카테고리. Y가 두 임계 값 사이에 있으면 해당 클래스에 할당됩니다.
이러한 임계 값을 결정하기 위해 감독되지 않은 기술을 사용했습니다. 먼저, 반올림 값에 가까운 신호를 걸러 내고 (많은 노이즈가 존재하지 않음) 반올림 값을 레이블로 사용했습니다. 그런 다음이 반올림 된 값의 분포를 결정하고 유사한 분포를 생성하도록 임계 값을 선택했습니다.
약간의 블렌딩
이 HMM의 많은 변형들이 경쟁 과정에서 만들어졌습니다. 저의 팀원 Zidmie는 그의 스크립트에 카운터를 사용했으며 최종적으로 342개가 만들어졌습니다. 경쟁이 진행되는 동안 우리는 CV 점수와 공개 LB 점수를 약간 개선했습니다. 연속 버전 간의 차이 수가 CV 점수의 차이보다 훨씬 높은 경우가 많으므로 새 버전에서 변경 한 내용이 모두 정확하지는 않습니다. 따라서 우리는 계산 된 확률을 사용하여 서로 다른 순방향 알고리즘의 결과를 함께 혼합했습니다. 이것은 우리에게 약간의 증가를 주었다.
마무리
나는 우리의 최종 결과를 매우 자랑스럽게 생각합니다. Kaggle에서 자주 볼 수있는 1001 가지 모델의 전형적인 앙상블이 아니며 1 시간 이내에 실행된다는 점을 고려하면 솔루션이 다소 우아하다고 생각합니다. 또한 경쟁 조직의 코드를 사용하여 추가 데이터를 생성하거나 데이터 생성 프로세스를 리버스 엔지니어링하지 않았습니다. 결국, 우리가 아닌 다른 팀에서 발견 한 누출로 인해 2등이나 떨어져서 약간 실망했습니다. 그럼에도 불구하고, 나는 이전에 히든 마르코프 모델을 사용한 적이 없었고 2 명의 똑똑한 사람들을 알게 되었으므로 이 대회에서 많은 것을 배웠습니다!
이 대회에 다시 한 번 감사드립니다.
출처
- https://www.kaggle.com/c/liverpool-ion-switching/overview
- https://en.wikipedia.org/wiki/Ion_channel
- https://www.nature.com/articles/s42003-019-0729-3
- https://papers.nips.cc/paper/1144-factorial-hidden-markov-models
- https://github.com/hmmlearn/hmmlearn
Member discussion